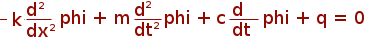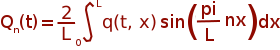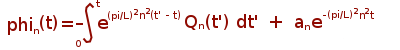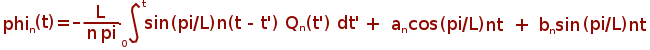1D Linear Differential Equations With Time - FEM Approach

1D - Initial – boundary value problem

Initial - boundary value problem to solve

where external force


for x in [0, L] and initial condition is imposed by the function phi(0, x) with the boundary conditions: phi(t, 0) = phi(t, L) = 0 for each t.

The analytical solution can be represented as an infinity sum:

together with

where

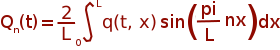
Let's consider two basic examples:

1. First Order Differential Equation in Time.

   m = 0, c = 1, k = 1 then the solution reads:
   
   

   
   
   a_n constants must be determinated from the initial condition. The analytical solution can be approximated by the example1.m program: function [initial, result] = exact_time_example1(N, Q, T, x, varargin)
   input arguments:
   • N - the upper limit in the main sum
   • Q - force as anonymous function
   • T - time at which the solution is obtained
   • x - grid; to make it use npoints.m
   • varargin - optional input arguments to define other (then t and x) arguments in Q(t, x , ...) function
   output arguments:
   • initial - the first initial condition i. e. phi(0, x) that is used to compute the result
   • result - an approximation of the analytical solution obtained at each point of x-grid and at time T
   The outputs can be used in below-described programs to compare exact solution vs. numerical ones.

2. Second Order Differential Equation in Time.

   m = 1, c = 0, k = 1 and imposing the second initial condition i. e. dphi(t, x)/dt at t = 0 the solution reads:
   

   

   a_n and b_n constants must be determinated from the initial conditions. To compute the analytical solution one can use example2.m program: function [initial, initial2, result] = exact_time_example2(N, Q, T, x, varargin)
   input arguments are the same as above
   output arguments has one more variable named initial2 that is the second initial condition i. e. dphi(t, x)/dt at t = 0.

A questions to answer: What is the main difference between both functions being exact solutions? Apart from the obvious one i. e. they are solutions to differential equations of different order in time. The answer allows to choose a proper grid and other parameters necessary to compute the FEM solution.

Finite Element Method - Weighted Residual Approach

A numerical solution can be obtained with help of fem1D_time_weighted.m program (written in Octave (Matlab)).

fem1D_time_weighted.m - program consists of the function fem1D_time_weighted(L, h1, NL, NI, NR, phiLF, phiRF, q, phiInitial, phiPrimInitial, W, dt, T, tplot, varargin) where input arguments are:

• L - domain length
• h1 - length of edge compartments
• NL - number of edge compartments at the left side
• NI - number of internal compartments
• NR - number of the edge compartments at the right side
• phiLF - anonymous function describing left boundary, could be constant e.g. @(t) (0*t)
• phiRF - anonymous function describing right boundary (as above)
• q - force as anonymous function: @(t, x, L)(-2*x/L + 1)
• phiInitial - the first initial condition i. e. value of phi(t, x) function at t = 0
• phiPrimInitial - the second initial condition i. e. value of dphi(t, x)/dt at t = 0
• W - weighting function W(t) as anonymous function e.g. linear: @(t) t
• dt - time step
• T - the upper time limit
• tplot - a time number for which the plot is drawn
• varargin{1} - analytical solution as vector computed at the same grid points for the tplot moment in time (program to make grid npoints.m)
• varargin{2} - k coefficient
• varargin{3} - c coefficient
• varargin{4} - m coefficient

Finite Element Method - Taylor Collocation Method

Alternatively, a numerical solution can be obtained with help of fem1D_time_Taylor.m program (written in Octave (Matlab)).

fem1D_time_Taylor.m - program consists of the function fem1D_time_Taylor(L, h1, NL, NI, NR, phiLF, phiRF, q, phiInitial, phiPrimInitial, beta, dt, T, tplot, varargin) where input arguments are:

• L - domain length
• h1 - length of edge compartments
• NL - number of edge compartments at the left side
• NI - number of internal compartments
• NR - number of the edge compartments at the right side
• phiLF - anonymous function describing left boundary, could be constant e.g. @(t) (0*t)
• phiRF - anonymous function describing right boundary (as above)
• q - force as anonymous function: @(t, x, L)(-2*x/L + 1)
• phiInitial - the first initial condition i. e. value of phi(t, x) function at t = 0
• phiPrimInitial - the second initial condition i. e. value of dphi(t, x)/dt at t = 0
• beta - p-length vector consists of a set of beta parameters (each of them belongs to [0, 1]) used in time expansion; p - is a order of differential equation in time
• dt - time step
• T - the upper time limit
• tplot - a time number for which the plot is drawn
• varargin{1} - analytical solution as vector computed at the same grid points for the tplot moment in time (program to make grid npoints.m)
• varargin{2} - k coefficient
• varargin{3} - c coefficient
• varargin{4} - m coefficient

Help

To understand the above – presented algorithms you should know the meaning of expanding functions in terms of the Taylor series.
With help of the presentation and basic math try to find both numerical algorithms for the second – order problem. Then compare your findings with the programs.

Last update: February 22, 2020
© 2013-2020 taketechease.com Privacy Policy Terms of Use