The domain Ω is a set of points in two – dimensional Euclidean plane ℜ2. The initial mesh should define the shape of the domain Ω or more precisely its boundary ∂Ω. Let us denote the bd(Ω) as Γ. It could form a smooth curve (like a circle) or be a polygon. At the beginning it is necessary to assign the initial set of nodes belonging to Γ. Taking into account polygon it is obvious that the initial mesh must consist of its vertices, however, in the case of a smooth curve one can choose the initial mesh differently. In the article, the author concentrate on the polygonal domains (see Fig. 1) that can be formed from a smooth curve after placing some initial nodes on its boundary Γ and connecting them by line segments (chords).
Fig. 1. Figure presents the domain ΩA and its boundary ΓA after projection to the polygonal domain. It has eight boundary nodes and one central node. Comparing both the initial Ω and the polygonal ΩA domain one can notice that such a simple projection gives rather rough correspondence between them a), however, in some cases it could be a sufficient one i. e. when an integrated function changes very slowly in some δ – thick neighbourhood of the boundary Γ b).
Let us start with determining the principal rectangular superdomain as a cartesian product
where the domain Ω is embedded in this super-domain. This object is introduced due to a mesh creation procedure presented in the here.
The following function meshinit (vertices, radius) where the variable vertices determines the number of its sides and the second one gives the radius of its circumscribed circle. For instance, one can make use of the Octave GNU project (free open source) and create both the initial nodes p and the initial triangles t arrays in the case of regular polygon of N vertices and lying within a circumscribed circle with a given radius.
Following further steps of the algorithm presented in next sections, one can obtain meshes for different domains Ω (see few examples in Fig. 2).
Let us introduce a measure that estimates an element area in respect to the prescribed element area S designed by the element size h. The measure SN = Selem/S gives a normalized area for each element. An estimation of the average deviation from assumed value of the element area provides information of mesh quality in the case for their fairly uniform distribution.
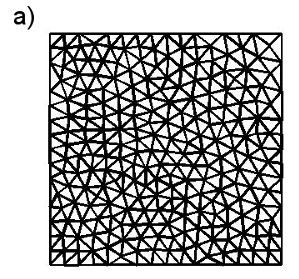
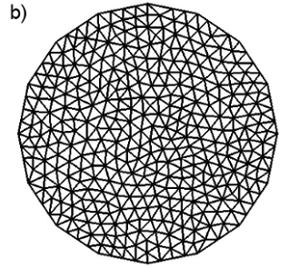
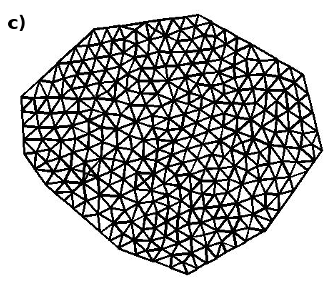
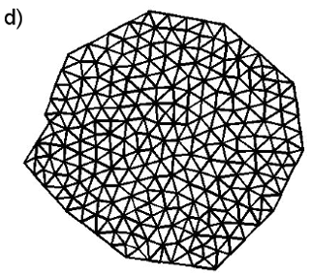
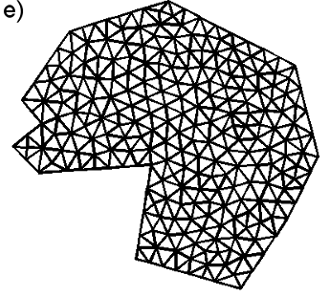

Fig. 2. Figure shows four domains Ω having different shapes. In brackets, finally established set of parameters is written: Np – number of mesh points, Ndivisions – number of divisions (according to Sec. 3.2), SA, N – a normalized average element area are presented; a) regular polygon – square (258, 8, 1.002); b) regular polygon with 16 nodes (376, 6, 1.026) which approximates circular shape well; c) non – regular, convex figure (315, 8, 1.01); d) non – regular, semi – convex figure (247, 6, 1.071); and two non – regular, non – convex figures e) (245, 7, 0.993) and f) (164, 6, 1.0003) both with weight = [0.25, 0.75].