The algorithm of Grassberger and Procaccia (Phys. Rev. Lett. 50, 346-9) allows to find both the embed dimension and the correlation dimension in a single computations. When an attractor is embed in growing dimensions starting from 1 then its correlation dimension dG grows as well up to some critical value. The correlation dimension is computed from the correlation function
| N | ||
| C(R) = limN → ∞ [ 1 / N2 | ∑ | H(R - |xi - xj|) ] |
| i,j=1 |
where R is a correlation sphere radius and H denotes the Heaviside's function. |xi - xj| is a distance between two points from the attractor.
In the optfinderML user should set ranges of the sphere radius and parameters for the attractor reconstruction via the Time Delay Technique i.e. the assumed value of the time delay and a final value of the embed dimension up to which program will compute the correlation dimensions.
|
On the basis of C(R) function the correlation dimension is computed from the log-log plot of C(R) function as
at small R. The dG with the growing embed dimension reaches its limit value. Further increasing of embed dimensions D does not change the correlation dimension (see figure below).
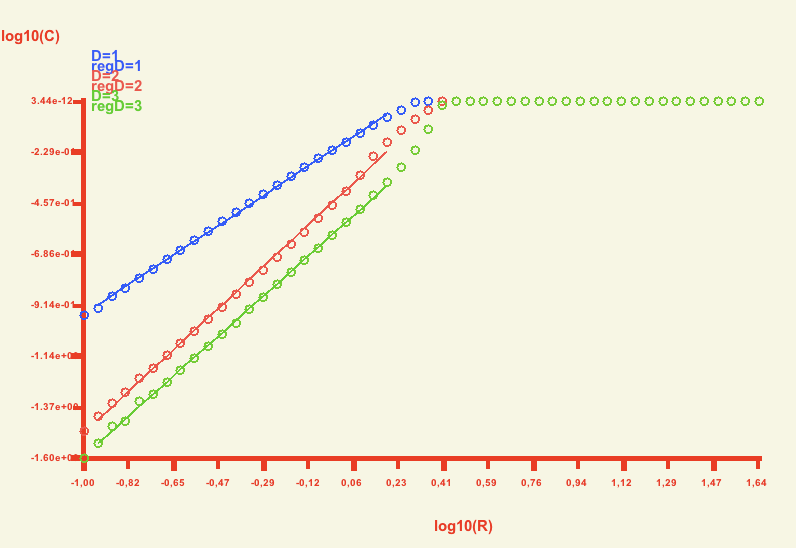
|
Obtained values of the dG correlation dimension are as follows:
In the optfinderML, uncertainty of regression can be shown in the graph. In all presented cases, computed error lines are too close to regression lines and they are not seen as different from the central regression lines. Thus for better figure's clarity error lines are not plotted in the picture above.
Package for machine learning - OptFinderML.