A collision is such an interaction of entities during which one body bumps into another one, and after remarkably short period of time their velocities changes.
The line of collision is the line that is normal to surfaces of both interacted entities and goes through the collision point (see Fig. 1 - rigid balls collision).
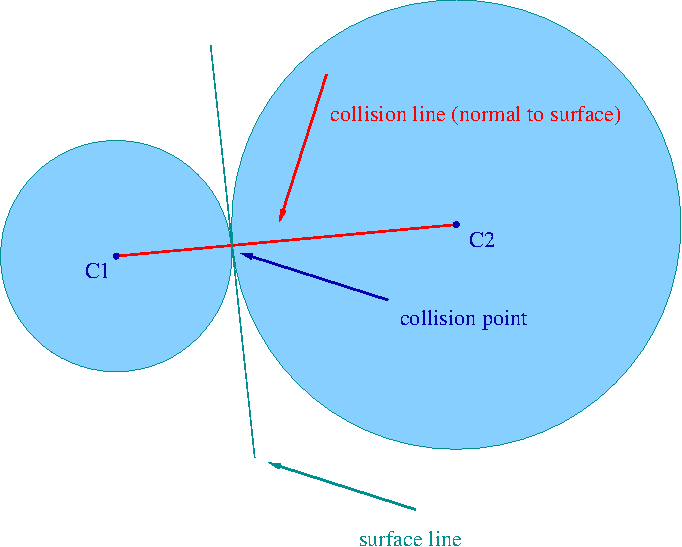
A collision is called the central collision if at the moment of collision mass centres (C1 and C2) of both interacting entities lies on the collision line.
A collision is called the simple collision if before the collision velocities (v1 and v2) of both interacting entities are parallel to the collision line.
During a collision a system of interacting entities forms a closed system (in approximation). It means that momentum, rotational momentum and energy of the system are conserved.
A closed system is a system that does not interact with external entities i. e. entities outside the system and no external force acts upon the system.
Momentum p is a vector quantity defined as product of mass and velocity of a material point. Momentum of a system of n material points is a vector p being the vector sum of momenta of all material points forming the system:
| n | ||
| p = | ∑ | pi |
| i = 1 |
Momentum of a whole system is a product of the whole system mass M and its mass centre velocity VC:
Rotational Momentum of a material point is considered in the relation to immobile point in the space (O point). Rotational momentum is then defined as a cross product of the vector r linking point O and the material point and the momentum p of the material point:
Rotational Momentum of a body (e. g. ball) can be considered in the relation to immobile point in the space (O point) around which the body is rotated with the rotational velocity ω. Rotational momentum is defined as
| L = | ∫ | r ✗ v dm = | ∫ | [r ✗ (ω ✗ r)] dm |
| m | m | |||
where the vector r links the point O with the small mass element of the body (dm where m denotes total mass of the body). And the vector v is velocity of this mass element given by v = ω ✗ r.
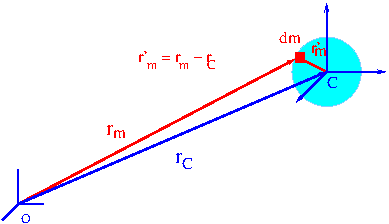
Rotational Momentum of a body considered in the relation to immobile point in the space L and rotational momentum of a body considered in the relation to its mass centre LC (which can move in the translational manner) are
where the vector rC is the vector linking the body mass centre with the immobile point O and the momentum vector p is the body momentum in the inertial system of coordinates (see Fig. 2 - systems of coordinates).
Energy E is a scalar quantity being a general measure of various forms of motion considered in physics. Energy of a system describes this system in respect to possible changes of motion. These changes occurred due to interactions between parts of the system or interactions between the system and external environment.
Mechanical energy Em is energy of motion and interaction:
where Ek is kinematic energy (energy of motion) and Ep is potential energy of various interactions (i. e. interactions between system entities and between system entities and external world).
Momentum p of a closed system does not change in time:
| dp | ||
| — | ≡ | 0 |
| dt | ||
It gives that p (vector!) is constant. The considered conservation law is an implication of Newton's laws of motion because the rate of change of momentum in time equals the external net force acting upon a closed system. As it has been written, the net external force acting upon a closed system is 0.
Rotational Momentum p of a closed system considered in relation to an immobile point in the space does not change in time:
| dL | ||
| — | ≡ | 0 |
| dt | ||
It gives that L (vector!) is constant. It means that, for instance, the rotational momentum of ball in relation to its mass centre does not change in time.
The considered conservation law is an implication of Newton's laws of motion because the rate of change of rotational momentum in time equals torque of the external net force acting upon a closed system. As it has been written, the net external force acting upon a closed system is 0.
Mechanical energy Em of a closed system is conserved (i. e. does not change in time) if no internal non – potential forces present in this system do work.