Mathematical Software - Chaotic Systems - Poincare Map
Poincare Map
Definition
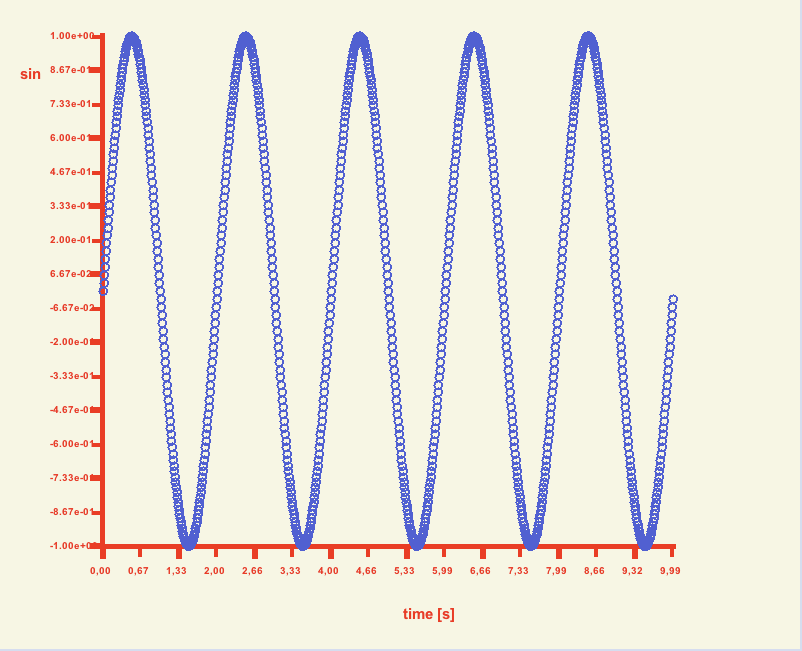
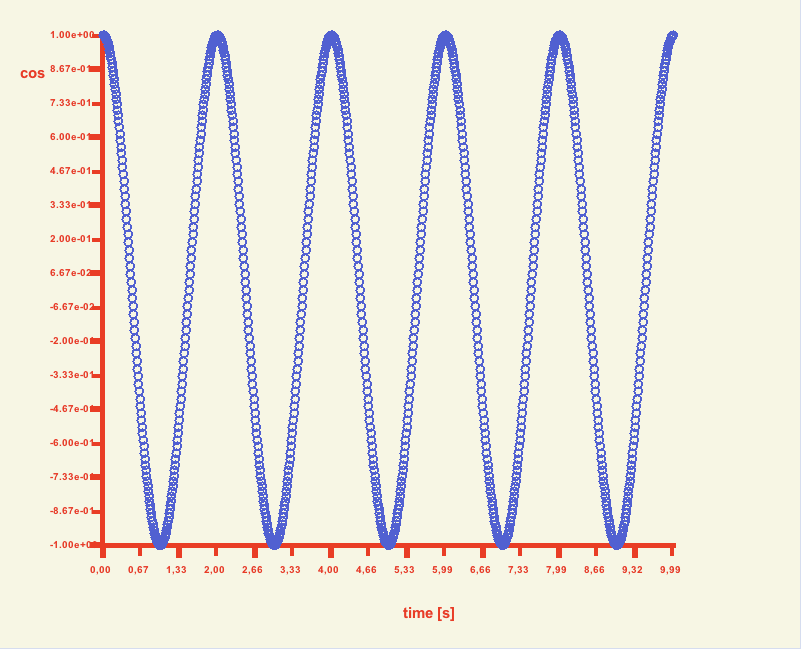
The Poincare's method is based on collecting values taken from a time series with a mapping period Tm and corresponding mapping frequency ωm = 2π/Tm. If two trajectories are observed
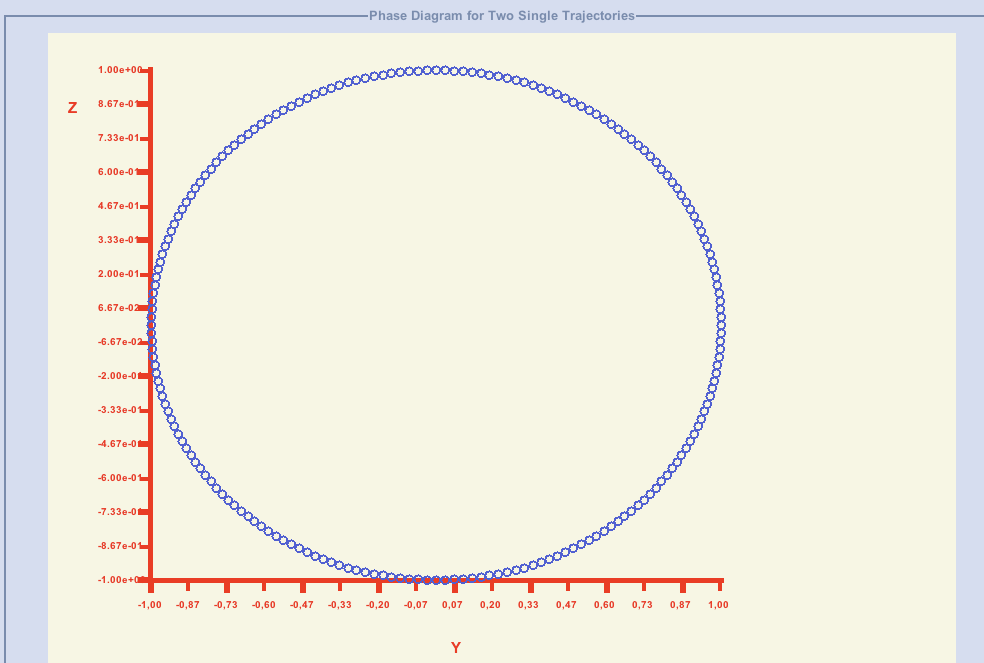
then obtained data form 2D pointal coordinates giving the phase portrait
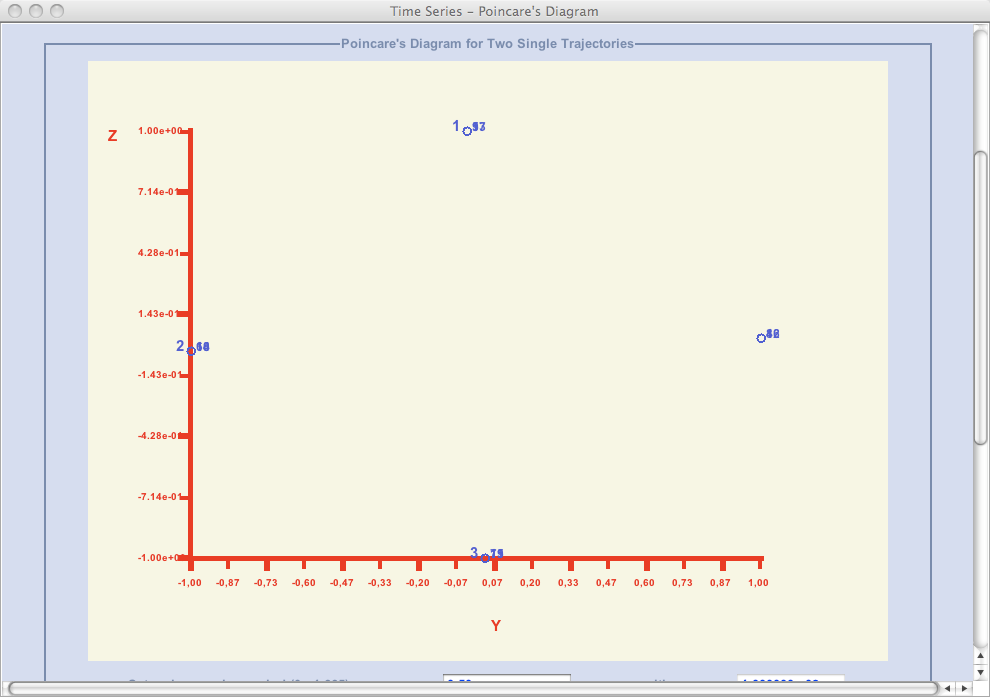
whereas Poincare points (obtained with the mapping period Tm ) are depicted on a graph below together with numbers representing their ordering:
Both a number of repeated pointal positions seen as different
(q) and order of their occurrence matter. Namely, computation of the characteristic frequency is based on the expression
ω0 = p/q ωm
where p is a sum of a number of skipped over positions counted in the counter-clockwise direction between two successive points and 1.
Chaotic Systems - References
- ^ G. L. Baker, J. P. Gollub, Chaotic dynamics: an introduction, Cambridge University Press, 1996
- ^ Vadim S. Anishchenko et al., Nonlinear Dynamics of Chaotic and Stochastic Systems, Springer-Verlag, 2007
- ^ Boris P. Bezruchko and Dmitry A. Smirnov, Extracting Knowledge From Time Series, Springer-Verlag, 2010
Machine Learning - OptFinderML
Package for machine learning - OptFinderML.