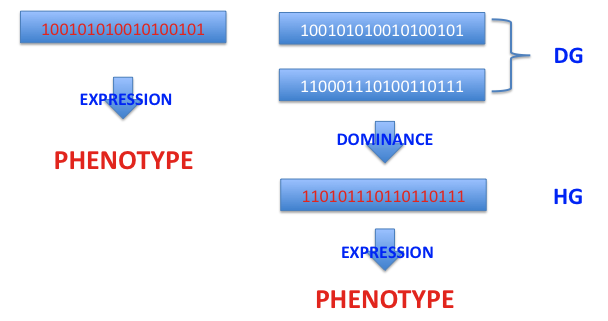
Genetic algorithms (GA), which are one of the numerical methods, are used to simulate computer genetic populations. Genetic algorithms (GA) can be divided into two types: haploid and diploid. Both genetic models deal with populations of sequences of bits. Each sequence represents parameter or set of parameters written as
a single binary string (constituting an artificial chromosome) in haploid GA
a pair of binary strings (a pair of chromosomes) in diploid GA.
Information from that genotype is decoded to a single numerical value or multiple values, which is called a phenotype. That decoding is often done according to commonly known representation of a positive integer as a sequence of bits. These integers are in the range [0, 2l - 1], where l - denotes the length of the bit sequence. In order to represent real numbers, this range should be mapped to a new [Umin, Umax] by a linear mapping. After doing so, the obtained numerical value (phenotype) is used to compute the desired function according to the mathematical formula determining the problem to be solved. Single parameter problems are represented by scalar functions, while more complex multi-parameter problems are described by vector functions. In the first case, a corresponding fitness function is computed from the scalar representation of the system. In the latter, the Pareto approach is often used (to learn more see The Pareto Condition.)
The fitness function is the primary measure of the strength of a chromosome for its occurrence in the next generation. The higher fitness of chromosome the greater chance to reproduce. Reproduction in population is thought as a randomised process based on the fitness function. Only those chromosomes that are selected will take part in creating the next generation. In haploid models, a chromosome pair is a parent pair that exchanges their genetic information in the crossover process, while in diploid models, the process of gametogenesis uses the crossover mechanism to exchange genetic information between gametes. Despite this slight difference between the haploid and diploid models, in both cases it is required to find the crossover point or points (in the multiple crossover models) on the two parent chromosomes with the assumed crossover probability. In addition to this random process, genetic information can be altered through mutations. Mutations are also random processes that occur with a certain probability. Genetic reconfigurations can also be applied to the chromosomes to increase the genetic variability of the newly created population.
Haploid (HG) genotypes are made up of single chromosomes, while diploid (DG) genotypes are made of pairs of chromosomes. In the latter case, the duplication of genetic material results in an enrichment of the process of genetic expression through the dominance mechanism, while in the haploid model individual chromosomes are directly decoded into phenotypes.
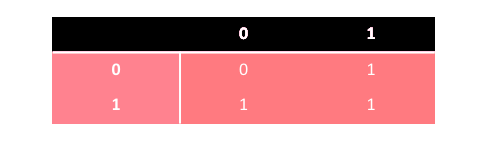
The dominance feature in simple diallelic genotypes can be represented as:
Diploid AG can be extended to triallelic genotypes where the bit of value 1 has two variants, i.e. the weaker type 1 R and the stronger type 1 D . The scheme of domination is presented in the following table

A fitness function is a non-negative criterion of quality computed for each individual chromosome in population. The better the fit the higher value of the fitness function. This feature of a genetic genotype can be used to find the optimal solution (i.e. numeric value) for some mathematical problems such as searching for a function's maximum or minimum. To do this, it is necessary to define the problem to be solved using a f(x) function which is the aim function for the problem under consideration. Let us analyse two issues:
the first issue concerns the minimum of a given function f(x). This problem corresponds to the following definition of the fitness function F(x):
where fmax constant provides a non-negative value of the function F(x).
the second issue concerns the maximum of a given function f(x). This time the fitness function F(x) is defined as:
where Cmin constant provides a non-negative value of the function F(x) e.g. Cmin = |fmin|.
Punishment function H is a penalty added/subtracted to/from the aim function f(x) when any of constraints are violated. Let's deal with two cases:
searching for the minimum of the function f(x) with constraints given by hi(x) functions where i = 1, 2, ..., n
| fnew(x) = f(x) + r | ∑ | H[hi(x)] |
where r is the penalty coefficient and the function H can be set as e. g. hi2(x).
searching for the maximum of the function f(x) with constraints given by hi(x) functions where i = 1, 2, ..., n
| fnew(x) = f(x) - r | ∑ | H[hi(x)] |
where r is the penalty coefficient and the function H can be set as e.g. hi2(x).
Scaling the fitness function allows the modification of the survival ability of the chromosome in the population. This is often done for two reasons. The first is to enhance the reproduction of weaker genotypes in the first generations. In this way, populations tend to reach the optimum more slowly and constitute a more flexible genetic population for longer. The second reason is the creation of larger differences between very similar genotypes in the final generations, when the average state of the entire population is very close to the solution sought. This improves the resolution of the method. The following types of fitness function scaling are used:
where a and b coefficients are found from two conditions:
conserving the average fitness i. e. Fsc, ave = Fave
the maximum fitness after scaling meets the condition Fsc, max = C Fave, where the multiplier C comes from the range [1.2, 2.0]
σ - truncation of the fitness function F(x)
where σ is the standard deviation of F and the constant C is in the range [1, 3].
power scaling of the fitness function
where the value of the power C depends on the problem.
A sharing function is a function of the distance between chromosomes in a population. The distance between chromosomes can be computed on the basis of their phenotypes or genotypes. When phenotypes are a measure of chromosomes similarity, the distance function is expressed by the formula
where xi and xj are phenotypes of i-th and j-th chromosome, respectively. Otherwise, when the computed distance reflects the similarity between two genotypes the Hamming measure is used. It is defined as the number of different bits at corresponding positions on both chromosomes of equal length divided by the length of the first or second genotype. The sharing function S(d) can be set as a linear or a power function of the distance dij between chromosomes i.e.
where the power p is a parameter of the genetic algorithm. The sharing function is computed to modify the fitness function Fi of i-th chromosome in the following way:
| Fi, sharing = Fi/ | ∑ | S(dij) |
where the sum is after j.
The application of the sharing function to the genetic algorithm leads to the division of the population into a set of sub-populations. By using a sharing function approach, species formation in genetic populations can be simulated. For this reason, in mathematical optimisation problems, the sharing function is used in the search for the optimum of multi-modal functions.
Having the entire population built taking into account the fitness factors computed for each chromosome in the population, the group of parents of the next generation can be selected. The mechanism of selection is based on one main rule the better the fitness, the greater the reproduction (more children). Reproduction can be done by one of the following methods:
deterministic: for each genotype its fitness factor (Fi/Fsum) is computed. Then the number of copies assigned to the i-th genotype is computed as the integer part of the number of copies expected
where Fi is the fitness of i-th genotype and n denotes the population size. The remaining vacancies in the new population are allocated to those genotypes with a larger floating-point parts of ni.
random based on rests - type I: first step is the same as for deterministic selection. The remaining vacancies in the new population is taken by the roulette method. The roulette is built from the floating-point parts of fitness factors.
In each case, selection is done up to complete the new population.
Crossover is a process that is applied to a pair of chromosomes. As the first step, the crossover point is selected randomly with the assumed probability. This point defines the position of the dividing bit on both chromosomes. The bits taken before the crossover point from the first chromosome are merged with the bits from the second chromosome at and after that point. Thus, a new genotype is created. The second genotype of the new pair is formed equivalently. In the example shown below the crossover point is 5.

Mutations are applied to each new chromosome with a certain probability. If a mutation occurs the bit value is changed to the opposite value i.e. 1 → 0 and 0 → 1 in diallelic models, while in triallelic ones this change looks like this: 1R → 1D or 1R → 0.
Reconfigurations are applied to chromosomes that have more than one gene. In such cases, the location of the allele (locus) on the chromosome may not be constant. It may vary depending on the reconfiguration used. The following list shows the main types of reconfiguration:
partially matched crossover: two chromosomes exchange genetic information. The matching section is indicated by two points randomly found. Then alleles on both chromosomes in the matching section create a map that is used to construct new chromosomes through transpositions. The numbers below present alleles located in an ordered way on a chromosome. So far alleles have been arranged on the chromosome from the first to the last, that is, from 1 to 9. Now the order of the alleles can be permuted.

order crossover: the matching section is indicated by two points randomly found, as previously. Then alleles in the matching section form a map of transpositions. The alleles in the section are substituted by holes (H).
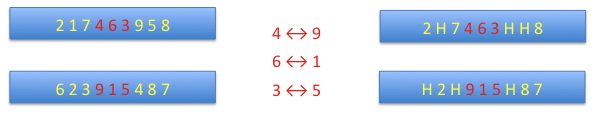
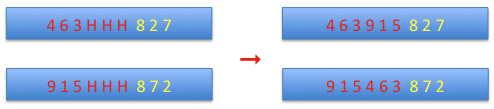
Then the part before the matching section is added to the part after it and the holes are shifted to the matching section and replaced by alleles from the matching section of the complementary chromosome.
cycle crossover: at the beginning the first alleles from both chromosomes are set as the starting values, and the corresponding allele from the complementary chromosome is set on the current chromosome. This continues until the starting allele is reached.
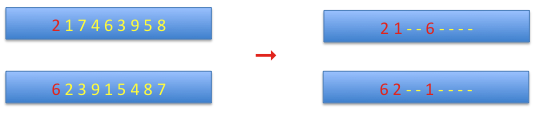
The remaining sites are defined by the complementary chromosome.

The Pareto condition says that the vector x is smaller (partially) than the vector y when the following condition
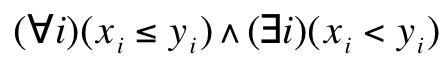
is satisfied where xi and yi are the i-th components of the vectors x and y, respectively. This means that the y point is dominated by the x point. If a point is not dominated by any other point, it is called the non-dominated point. These vectors may represent F fitness vectors F belonging to different chromosomes in the population. Then problem of finding better solutions on the basis of higher value of the scalar fitness function is replaced by a search for a group of chromosomes meeting the above-written condition. The Pareto condition, due to the way it is formulated, can naturally be applied to find the minimum of a function. When the opposite problem is put forward a fitness vector must be multiplied by -1. Then the above-written condition can be used straightforward.
That part of chromosomes that satisfies the Pareto condition must have the same reproductive power because this procedure should not discriminate against any of the non-dominated chromosomes. For this, a specific selection algorithm is used, quite similar to the Wetzel's method mentioned above, but this time the ranking depends on the degree to which the chromosome is not dominated. All not-dominated chromosomes have the same rank value in the selection routine. Having selected the first group of Pareto-positive chromosomes with the rank 1, the next one can be selected in the same manner within a sub-population of Pareto-rejected chromosomes. The group of genotypes has assigned the next rank value i.e. 2, obviously. The lower the rank, the greater the number of children associated with it. This process continues until rank values are found for all chromosomes in the population.
For better results, the multi-parameter Pareto-based problems can be associated with the technique of forming species (e.g. using a sharing function approach).
Genetic Search Package - OptFinder.
To partially test this software, go to Online Optfinder Page.
Genetic algorithms (GA) also play an important role in Genetic Based Machine Learning Systems. One type of these systems is called the Classifier System.
Classifier systems are systems that learn certain rules of conduct in given circumstances. They are built from the following subsystems
a rule and message system
a credit algorithm
a genetic search system (GA)
To learn more go to machine learning page.